本所劉致為教授榮膺「第二十二屆有庠科技講座（奈米科技）」，特此恭賀！

本所林恭如教授榮獲「國科會工程處113年度產學合作計畫成果發表暨績效考評會—海報組特優獎」，特此恭賀！

本所吳肇欣教授榮獲「中國電機工程學會113年度傑出電機工程教授獎」，特此恭賀！

本所11月份演講公告：

3D Staggered PSTD Modeling of Structural Coloration in Morpho Butterfly Wings

Professor Snow H. Tseng's Laboratory

Graduate Institute of Photonics and Optoelectronics, National Taiwan University

臺灣大學光電所 曾雪峰教授

Simulation analysis of the vivid structural colors of Morpho butterfly wings, utilizing three-dimensional staggered pseudospectral time-domain (PSTD) techniques. By overcoming the computational limitations often associated with traditional finite-difference time-domain (FDTD) methods, the PSTD model reduces the grid resolution required for accurate 3D simulations.

By leveraging staggered PSTD, we achieve high-fidelity results while mitigating the Gibbs phenomenon, providing more precise visualizations and insights into how light interacts with these microstructures. Reflectance and luminance analyses are employed to investigate the optical mechanisms. The findings are translated into RGB representations for intuitive visualization, offering insights into the structural color phenomena observed in Morpho wings.

Reference:
[1] https://commons.wikimedia.org/wiki/File:Morpho_rhetenor_rhetenor_MHNT_dos.jpg.
[2] Kinoshita, S. and S. Yoshioka (2005). "Structural colors in nature: the role of regularity and irregularity in the structure." ChemPhysChem 6(8): 1442-1459.

— 資料提供：影像顯示科技知識平台 (DTKP, Display Technology Knowledge Platform) —

— 整理：林晃巖教授、郭權鋒 —

基於學習型超穎表面的360°結構光

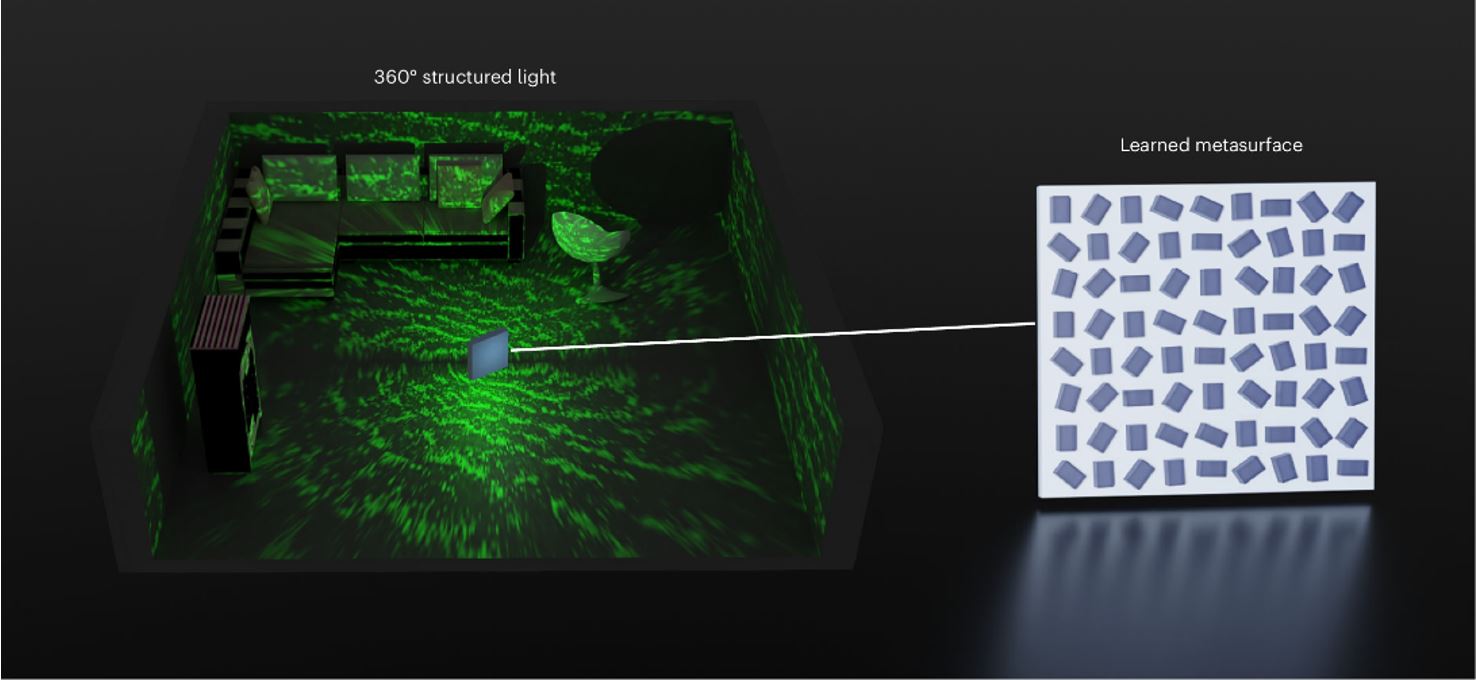
結構光技術旨在通過波前調制投影特定的光圖案，已應用於包括三維成像、全像顯示、光探測與測距，以及擴增與虛擬實境[1]顯示等多個領域。繞射光學元件（Diffractive optical elements, DOE）和空間光調制器（spatial light modulators, SLM）結合雷射照明，傳統上被用來實現結構光[2-4]。然而，最近的方法利用了端到端（end-to-end）的計算優化技術，實現了對多種圖案的高擬真度投影，在基於SLM的動態全像顯示[5-7]和基於DOE的三維成像[8]中已有展示。這些方法面臨一個根本的限制：由於DOE和SLM的微米級結構導致的有限繞射角度，可視範圍（Field of view, FOV）受到限制。這一限制阻礙了結構光在新興的360°三維成像和顯示技術中的應用，如擴增實境（AR）設備、機器人、自主車輛和人機交互等領域。

來自韓國浦項工科大學的團隊提出了一個可微分框架，該框架包含一個計算效率高的180°波傳導模型和特定功能的重建元件，並研發超穎表面的透射和反射通道。透過可微分框架中的一階優化項，優化了超穎表面的設計，從而實現了360°結構光。又將360°結構光應用於全像投影和三維成像。具體而言，該團隊展示了第一個360°光投影的影像，這得益於他們的傳導模型，其計算速度比Rayleigh–Sommerfeld傳導快50,000倍。在三維成像方面，深度估計準確度的以均方根誤差計算，相較於啟發式設計（heuristically designed）的結構光提高了5.09倍。這種360°結構光為機器人、延展實境（XR）系統以及人機互動提供了360°成像和顯示應用。

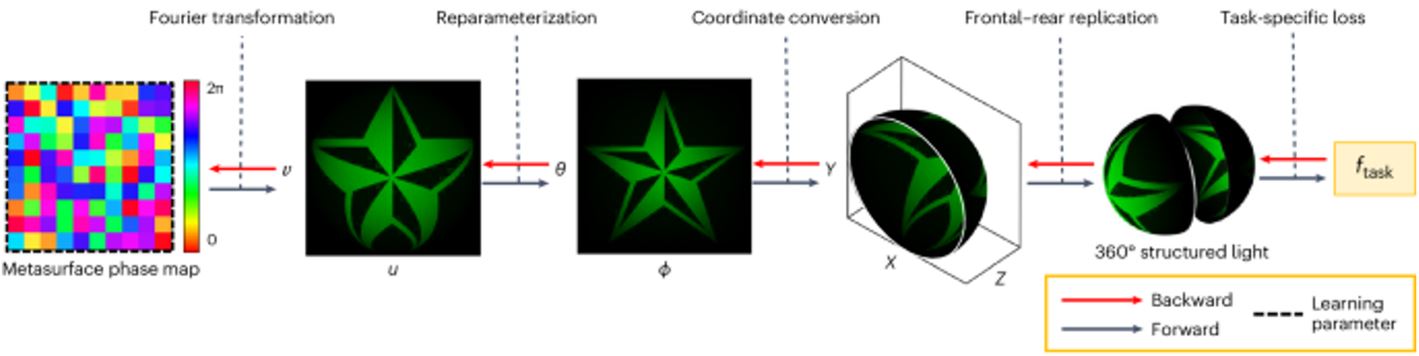
在本文中，作者提出了一種可微分且計算效率高的波傳導模型，能夠描述光與超穎表面相互作用後傳導至180°遠場波前的過程。圖二展示了傳導模型的計算過程。透過全波時域有限差分模擬（FDTD）研究了基於純量的傳導模型，這能夠檢驗去極化效應和超穎表面原子之間的近場耦合效應。

主動式立體是一種三維成像模式，採用多視角相機和結構光模組。投射的結構光可作為對應匹配的有效表徵，即使對於具有複雜視覺紋理和幾何形狀的觀看環境，也能實現多視角三維成像[9]。在這裡，作者利用360°結構光進行360°主動式立體三維成像。以此優化超穎表面相位圖Φ和深度重建神經網路θ的參數，產生了適合三維成像的優化360°結構光。整體框架如圖三所示。

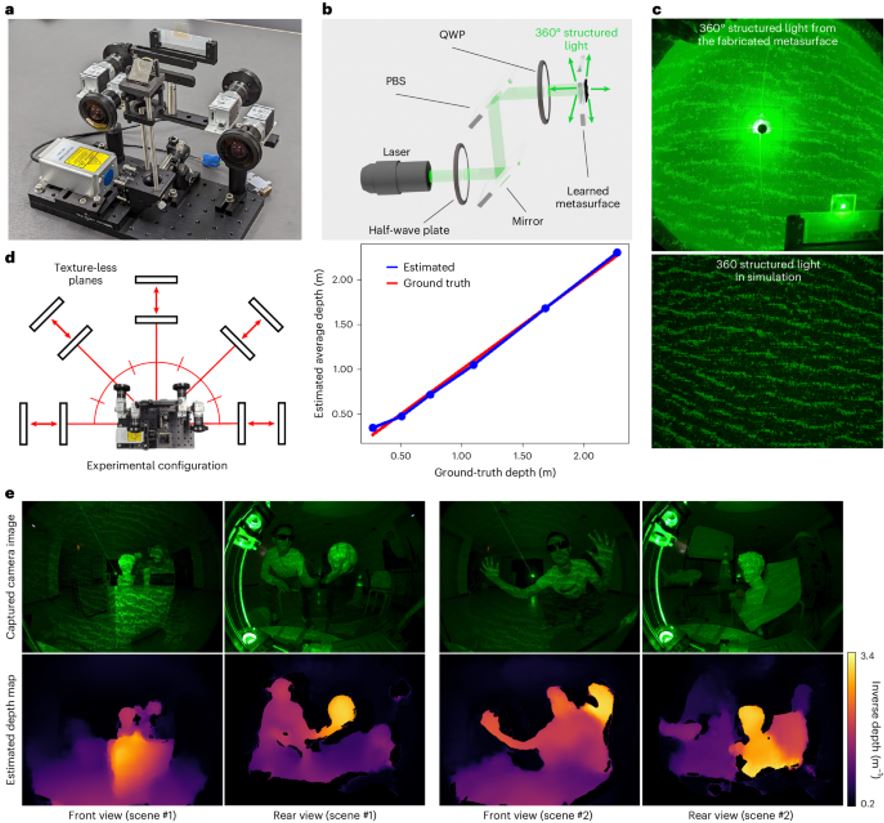
作者用學習型相位圖Φ製造了一個超穎表面來展示360°三維成像，如圖四(a)。構建了一個整合超穎表面照明模組和四個魚眼相機的實驗原型。360°結構光方法透過整合偏振光學元件來利用超穎表面的傳輸和反射通道。半波片改變線性偏振雷射的軸，以最大限度地提高偏振分光鏡（Polarizing beam splitter, PBS）的反射能量。現在水平線性偏振的光在通過四分之一波片（Quarter-wave plate, QWP）時發生狀態變化為左圓偏振，入射到超穎表面。在超穎表面的反射通道中，左圓極化轉換為右圓極化。特別的是，光軸附近的一些反射光會重新穿過QWP和PBS，但方向相反。偏振態在穿過QWP時發生變換，最終透過PBS傳輸。考慮到入射角範圍以及QWP和PBS的物理尺寸，作者所使用的原型能夠在不失真的情況下照亮反射區域。

對於全像光投影，作者成功地創建了高擬真360°光投影系統。儘管這些發現很有希望，但360°結構光的幾個方面還有待進一步改進。此外，開發高效的向量180°傳導模型仍然是未來研究的一個有趣領域，它將模擬大角度繞射下的去偏振效應。360°結構光是邁向嚴謹的360°成像和顯示的重要一步，為一系列應用帶來潛在優勢，包括機器人、擴增實境系統、人機互動和自動駕駛汽車。