本所刘致为教授荣膺「第二十二届有庠科技讲座（奈米科技）」，特此恭贺！

本所林恭如教授荣获「国科会工程处2024年度产学合作计划成果发表暨绩效考评会—海报组特优奖」，特此恭贺！

本所吴肇欣教授荣获「中国电机工程学会2024年度杰出电机工程教授奖」，特此恭贺！

本所11月份演讲公告：

3D Staggered PSTD Modeling of Structural Coloration in Morpho Butterfly Wings

Professor Snow H. Tseng's Laboratory

Graduate Institute of Photonics and Optoelectronics, National Taiwan University

台湾大学光电所 曾雪峰教授

Simulation analysis of the vivid structural colors of Morpho butterfly wings, utilizing three-dimensional staggered pseudospectral time-domain (PSTD) techniques. By overcoming the computational limitations often associated with traditional finite-difference time-domain (FDTD) methods, the PSTD model reduces the grid resolution required for accurate 3D simulations.

By leveraging staggered PSTD, we achieve high-fidelity results while mitigating the Gibbs phenomenon, providing more precise visualizations and insights into how light interacts with these microstructures. Reflectance and luminance analyses are employed to investigate the optical mechanisms. The findings are translated into RGB representations for intuitive visualization, offering insights into the structural color phenomena observed in Morpho wings.

Reference:
[1] https://commons.wikimedia.org/wiki/File:Morpho_rhetenor_rhetenor_MHNT_dos.jpg.
[2] Kinoshita, S. and S. Yoshioka (2005). "Structural colors in nature: the role of regularity and irregularity in the structure." ChemPhysChem 6(8): 1442-1459.

— 资料提供：影像显示科技知识平台 (DTKP, Display Technology Knowledge Platform) —

— 整理：林晃岩教授、郭权锋 —

基于学习型超颖表面的360°结构光

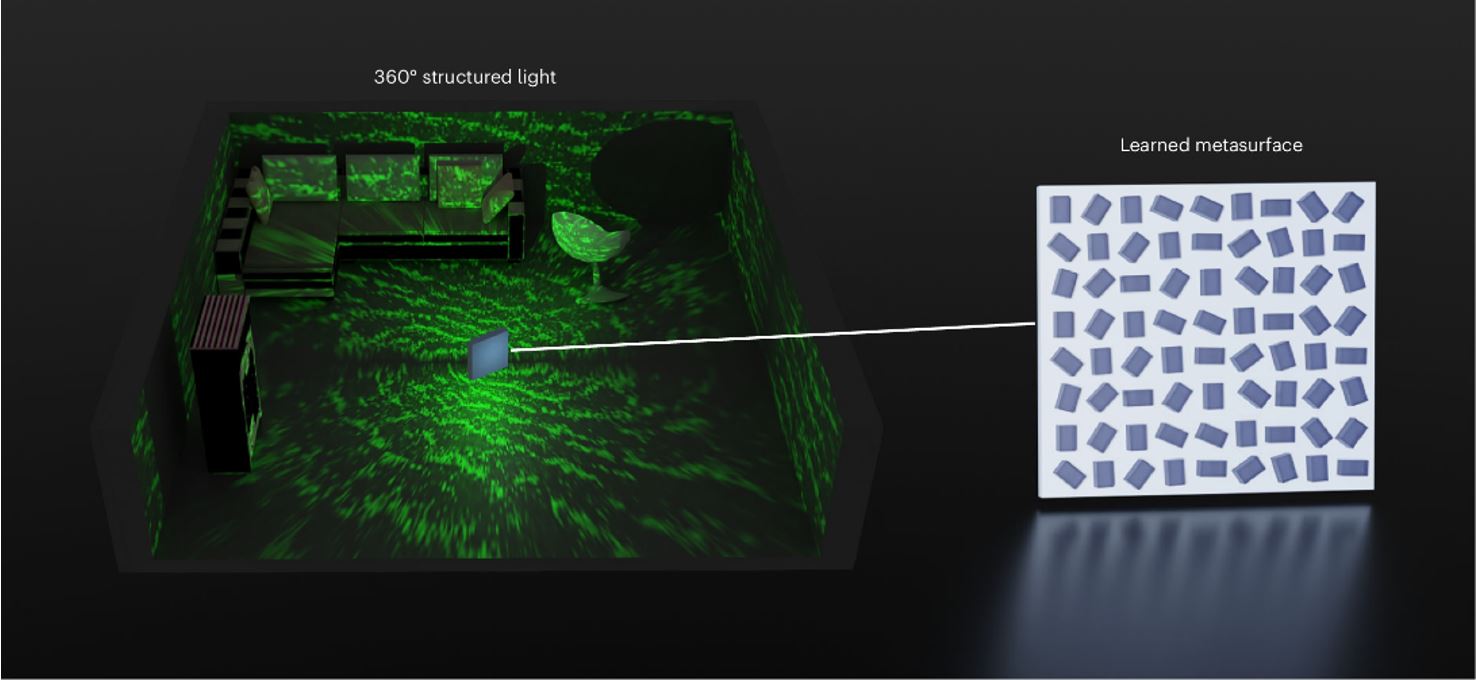
结构光技术旨在通过波前调制投影特定的光图案，已应用于包括三维成像、全像显示、光探测与测距，以及扩增与虚拟实境[1]显示等多个领域。绕射光学组件（Diffractive optical elements, DOE）和空间光调制器（spatial light modulators, SLM）结合激光照明，传统上被用来实现结构光[2-4]。然而，最近的方法利用了端到端（end-to-end）的计算优化技术，实现了对多种图案的高拟真度投影，在基于SLM的动态全像显示[5-7]和基于DOE的三维成像[8]中已有展示。这些方法面临一个根本的限制：由于DOE和SLM的微米级结构导致的有限绕射角度，可视范围（Field of view, FOV）受到限制。这一限制阻碍了结构光在新兴的360°三维成像和显示技术中的应用，如扩增实境（AR）设备、机器人、自主车辆和人机交互等领域。

来自韩国浦项工科大学的团队提出了一个可微分框架，该框架包含一个计算效率高的180°波传导模型和特定功能的重建组件，并研发超颖表面的透射和反射通道。透过可微分框架中的一阶优化项，优化了超颖表面的设计，从而实现了360°结构光。又将360°结构光应用于全像投影和三维成像。具体而言，该团队展示了第一个360°光投影的影像，这得益于他们的传导模型，其计算速度比Rayleigh–Sommerfeld传导快50,000倍。在三维成像方面，深度估计准确度的以均方根误差计算，相较于启发式设计（heuristically designed）的结构光提高了5.09倍。这种360°结构光为机器人、延展实境（XR）系统以及人机互动提供了360°成像和显示应用。

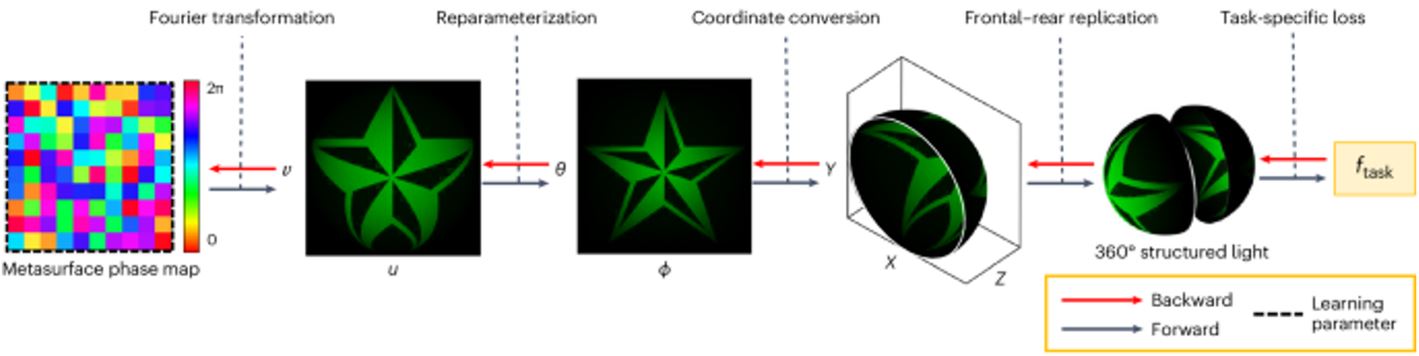
在本文中，作者提出了一种可微分且计算效率高的波传导模型，能够描述光与超颖表面相互作用后传导至180°远场波前的过程。图二展示了传导模型的计算过程。透过全波时域有限差分模拟（FDTD）研究了基于纯量的传导模型，这能够检验去极化效应和超颖表面原子之间的近场耦合效应。

主动式立体是一种三维成像模式，采用多视角相机和结构光模块。投射的结构光可作为对应匹配的有效表征，即使对于具有复杂视觉纹理和几何形状的观看环境，也能实现多视角三维成像[9]。在这里，作者利用360°结构光进行360°主动式立体三维成像。以此优化超颖表面相位图Φ和深度重建神经网络θ的参数，产生了适合三维成像的优化360°结构光。整体框架如图三所示。

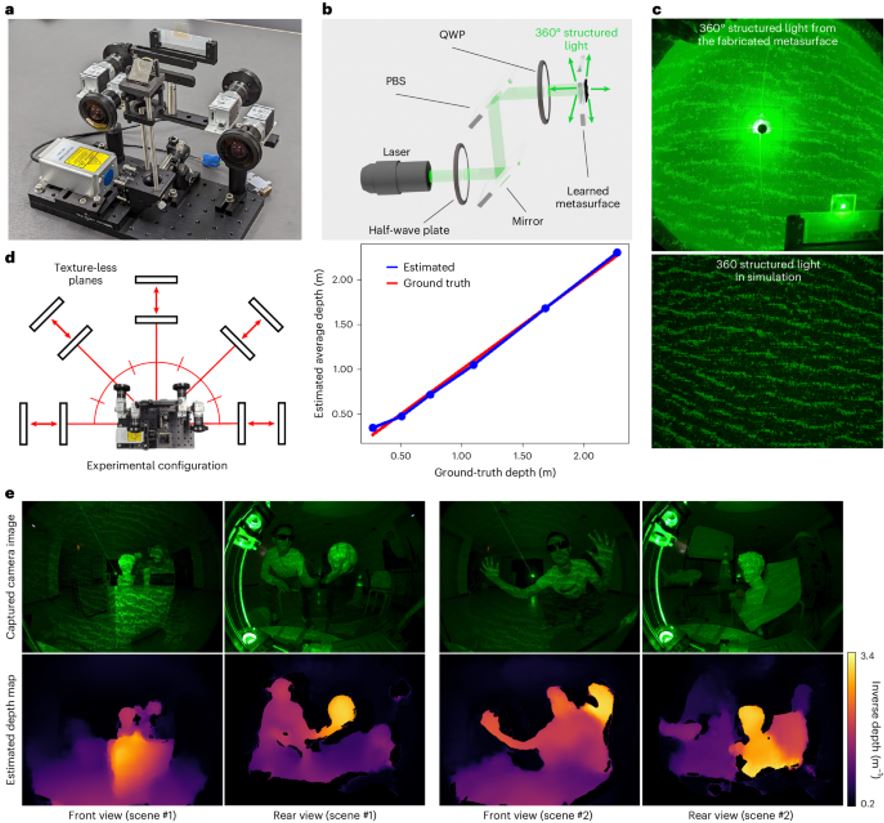
作者用学习型相位图Φ制造了一个超颖表面来展示360°三维成像，如图四(a)。构建了一个整合超颖表面照明模块和四个鱼眼相机的实验原型。360°结构光方法透过整合偏振光学组件来利用超颖表面的传输和反射通道。半波片改变线性偏振激光的轴，以最大限度地提高偏振分光镜（Polarizing beam splitter, PBS）的反射能量。现在水平线性偏振的光在通过四分之一波片（Quarter-wave plate, QWP）时发生状态变化为左圆偏振，入射到超颖表面。在超颖表面的反射通道中，左圆极化转换为右圆极化。特别的是，光轴附近的一些反射光会重新穿过QWP和PBS，但方向相反。偏振态在穿过QWP时发生变换，最终透过PBS传输。考虑到入射角范围以及QWP和PBS的物理尺寸，作者所使用的原型能够在不失真的情况下照亮反射区域。

对于全像光投影，作者成功地创建了高拟真360°光投影系统。尽管这些发现很有希望，但360°结构光的几个方面还有待进一步改进。此外，开发高效的向量180°传导模型仍然是未来研究的一个有趣领域，它将模拟大角度绕射下的去偏振效应。360°结构光是迈向严谨的360°成像和显示的重要一步，为一系列应用带来潜在优势，包括机器人、扩增实境系统、人机互动和自动驾驶汽车。