光子学与诺贝尔物理学奖

2021年诺贝尔物理学奖授予Syukuro Manabe和Klauss Hasselmann的“量化和可靠地预测全球暖化”，以及Giorgio Parisi的“发现从原子到行星尺度物理系统的无序和波动的相互作用”之贡献。

光在目前对气候变化的了解中扮演核心角色。我们星球的能量平衡被认为主要是由两种相反的机制驱动的，即以太阳可见光形式的能量吸收，以及以低频红外辐射形式的能量释放。在这场涉及反照率、散射和热反射的拉锯战中，光子学，特别是透过开发创新材料和效应，可以在限制全球暖化方面发挥重要作用。

可能不太符合预期和直观的是，有关于Parisi预测的无序和波动之间复杂的相互作用，光子学还有助于提供直接测试平台和实验证明。诺贝尔委员会在详细说明今年奖项的科学背景时，明确强调了光子学的这一角色[1]。这种相互作用的揭示可能是驯服复杂系统明显的不可预测性的关键。

在关于自旋玻璃理论（spin glass theory）的工作中[2]，Parisi研究了无序和波动之间的相互作用，并引入了复制对称性破缺（symmetry breaking）的概念。该机制涉及将统计力学概念扩展到表现出混乱和挫败的系统。优雅而强大，这个想法已经在自旋玻璃中找到了它的理论和数值实现，这是复杂系统科学四十多年中发展起来的建模里程碑[3]。一直难以捉摸的是对该效应的完整实验验证，包括复制对称性破缺的基本机制。这就是光子学介入的地方。

可实验的多模态非线性光学系统形成了自旋玻璃的物理实现。波动在光子学中扮演着核心作用。例如，它们决定了激光的线宽和成像系统的最终分辨率。然而，在非线性多模态光学系统中，内建无序和噪声之间的相互作用主宰系统行为。这已经在不同的框架中观察到，包括：高度非线性光纤、空间和时间孤子（soliton）、超连续谱产生和光束成丝等。

具有随机材料分布和强非线性光学状态系统的中心特征，是可观察量（例如光谱或散斑图案）的巨大可变性。这种可变性可能导致一个复杂光学系统的两个恒等的实现（即“两个复制品”）导致两个宏观上不同的响应，即便两实验是在完全相同的条件下进行的。例如，两个随机激光，有多种模态（空间和时间）和强烈地非线性相互作用为特征，即使它们是由同一种无序驱动，也可以显示完全不同的发射光谱（如图1）。事实证明，当能量增加到某个临界值以上时，在波动力学中有数种状态成立，结果是一种复杂形式的模态竞争(mode competition)与相关的所谓能源景观(energy landscape)。复杂性驱动的激光每次打开时都会锁定不同的状态，就像噪声可以耦合不同的自旋局部平衡配置一样，它可以导致随机激光从一种激光状态跳到另一种激光状态，从而增强波动并导致输出特征发生强烈变化。

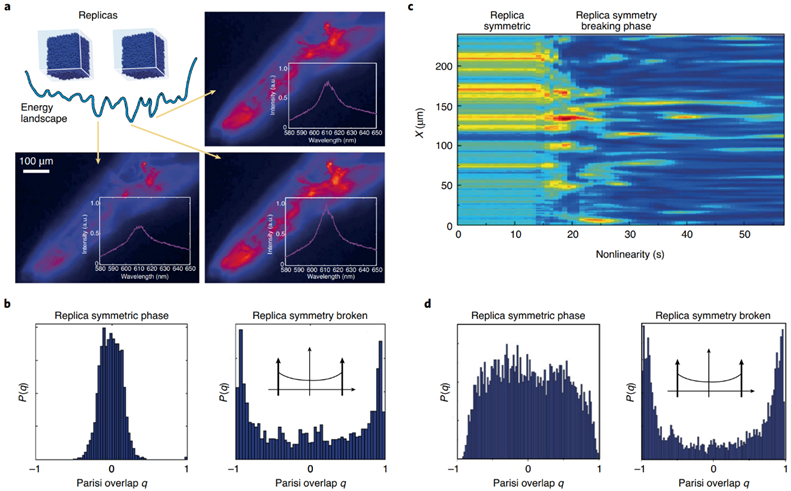
图1、光子学和复制对称性破缺。a. 相同随机激光实验的强度分布和光谱。波动不规律地推动系统透过“能源景观”中的众多竞争状态。b. 观察到的Parisi重迭的统计分布P(q) 显示了向双峰形状的特征过渡[9]。插图显示了自旋玻璃的模型案例[2,3]。c. 在非线性光束传播中，在非线性临界之上，输出强度分布经历向强烈波动状态的转变。d. 同样情况下，透过测量Parisi重迭的分布来证明复制对称性破缺[10]。（经知识共享授权许可改编的平台来自 CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/)：a,b, 参考文献9; c,d,参考文献10)。

在Parisi的概念框架中，能源景观是了解复杂行为真实本质的关键。为了证明这一点，他引入了所谓的帕里西重迭（Parisi overlap），这是一个可观测的量，它提供了破坏复制对称性的直接证据。尽管可以在数值实验中详细分析复制对称性破坏的机制，但在光子学中已经实现了对帕里西重迭所起作用的直接观察。

从2005年开始的一系列理论论文[4-7]中，引入了多模态非线性光学系统具有潜在能量景观的想法，在早期实验观察的证实了这一预测[8]。2015年，在随机激光中直接证明了帕里西重迭的特征分裂（图1），并且在2017年，于无序光折变(photorefractive)波导中的非线性光学传播中证明了这一点。正如诺贝尔委员会所叙述[1]，其它研究小组所重现的随机激光结果为“光子自旋玻璃”开辟了许多新问题和方向。

支撑光子自旋玻璃的核心概念是将模态幅度识别为复数“自旋”。在这些术语中，来自激光的光谱发射和光束的空间分布是由自旋确定的可观察量。透过测量同一系统的不同复制品的结果，我们可以计算 Parisi重迭的统计分布，即波动间的相关性。 Parisi预测，在复制对称性破缺处，从类高斯形状到双峰形状的特征转变在光子实验中非常清楚（图1）。

光子自旋玻璃立即提供了一类新的物理系统，用于测试复杂系统科学的基础和意外应用的基础。它们可能构成创新、高效率和环境友善的经典和量子计算硬件的支柱，作为解决组合优化和光子神经网络的大型Ising机器。