|
—
資料提供:影像顯示科技知識平台 (DTKP, Display Technology
Knowledge Platform) —
—
整理:林晃巖教授、陳聖灝 —
渾沌幫助能量的儲存
渾沌過程可以在動態系統中被觀察到,它的結果會隨著初始條件的不同而有很大的變化,1972年由Edward Lorenz 所提出「蝴蝶效應」的現象,之後陸續在各種書籍以及電影中流行起來。渾沌效應幾乎在所有的科學領域中被提及;在光學領域中,例如當一道擾動的光經過一個充滿非線性材料的共振腔,我們可以在此雷射二極體的輸出中觀察到渾沌現象;還有,在高菲涅爾數(Fresnel numbers)的雷射系統中,我們也可以在它的複雜時空型態(Complex spatiotemporal pattern)觀察到渾沌現象。
一個具有渾沌現象的系統,它的結果是無法預測的,因此通常在系統中我們不希望有這種現象存在;然而,渾沌現象的一些特性對於改善光學系統的表現是有幫助的,例如:高維度光學渾沌中加入一個具有渾沌濾波性質的同步耦合振盪器,可以使得訊息以每秒Gb等級的速率在超過公里等級距離的光纖系統網路中作保密傳輸;除此之外,利用隨機輸出與應用適當的後製方法來操作雷射,亂數產生的位元傳輸速率可以高於電子系統達到好幾個數量級。最後,這種在非對稱光學共振腔中的渾沌散射光之高亂度特性改善了微型共振腔雷射的輸出功率與光束的方向性。
現在,Liu等人在Nature Photonics中提出了光學渾沌的另一個好處
:它可以提高藉由寬頻光源激發的共振腔能夠儲存的能量,這個好處在兩個光學領域中引起了很大的興趣,第一個是高品質因子(通常定義為共振腔儲存的能量以及共振腔消耗的能量的比值)寬頻光學共振腔的開發,體積小、品質因子高、自由頻譜範圍大的微型共振腔對於開發低閥值微型雷射、極小濾波器和開關與腔內量子電動力學實驗等是非常關鍵的;第二個則是讓我們更了解渾沌共振腔—此共振腔的光學模態不受限於傳統規律週期軌道的限制,例如圓形共振腔的回音廊模態(whispering gallery modes,註1),因此這種共振腔內的渾沌波有著非常多且複雜的光線軌跡,這種共振腔產生與動態台球的軌跡具有許多相似特性;也是一個探討量子渾沌(例如渾沌穿隧)基本觀念的極佳系統。
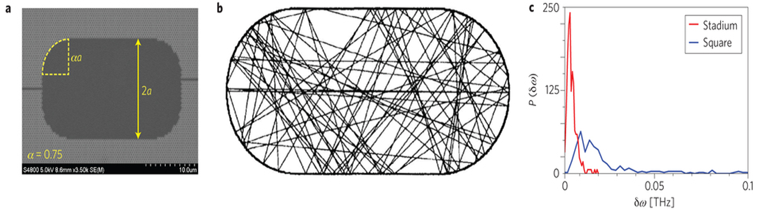
為了引進光學渾沌以及提高能量的儲存,Liu 等人製作了許多變形的介電質光學共振腔,圖1a為在一由在絕緣體上矽技術做成的平面光子晶體中的二維運動場型共振腔,研究學者設計此共振腔的幾何形狀和光子晶體的直徑使它具有1500奈米的能隙同時還有大約400奈米的頻寬,這種設計使得一個波長大約在1300到1700奈米的電磁波在此運動場型共振腔中不停地來回反射,後來Liu等人利用頻譜分析的方法來量測輸出中不同共振模態的譜線寬。
 |
|
圖1、運動場型光學共振腔的渾沌模態 a. Liu等人利用掃描式電子顯微鏡掃描出的運動場型共振腔圖像;b. 幾何光學中運動場型共振腔之渾沌軌跡;c. 方形與球場型共振腔的腔場模態譜線寬的統計分布圖。 |
|
|
|
圖1b所展示的問題是由Bunimovich首先做數學研究,其中,一道光以任一角度進入運動場型系統後會在邊界處經過許多次反射,此種光線具有複雜的渾沌軌跡;有兩個具有質量的小球分別以兩個稍微不同的起始位置進入球場型系統中,經由一段時間後,這兩個小球的軌跡將會急遽的發散,而這種系統可以由正的黎阿普諾夫指數(positive Lyapunov exponent)來描述(此函數定義了相鄰軌跡的發散程度),同樣的,它也可以被描述為具有非零但有限的Kolmogorov–Sinai 亂度,考慮這種光學系統,它意味著運動場型共振腔相較於傳統圓形或是長方形的共振腔可以有很大數量、生命期更長的光子共振模態,從耦合模態理論中我們可以發現共振腔中第i個模態的能量正比於光子的生命期如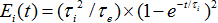 , ,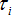 是第i個模態的生命期, 是第i個模態的生命期,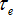 是此模態的逃脫速率,由於光子生命期與某一共振模態的譜線寬呈反比,譜線寬越窄的的模態場在運動場型共振腔中會比一般的方形共振腔的收集效果會更好。 是此模態的逃脫速率,由於光子生命期與某一共振模態的譜線寬呈反比,譜線寬越窄的的模態場在運動場型共振腔中會比一般的方形共振腔的收集效果會更好。
經過許多次量測不同形狀、截面積為400到1200μm2之共振模態譜線寬後,Liu 等人在此一變形共振腔中確實觀察到有更尖銳的峰值,此外,他們還發現所有模態的譜線寬幾乎都會收斂至某一特定值,在圖1c可以明顯看出來,此圖說明了球場型共振腔與方形共振腔某一譜線寬值與其機率的分布圖,相較於方形共振腔,渾沌共振腔的譜線寬會往較小的值偏移,這不只說明了共振模態的光子生命期的增加同時也說明了所有模態最後都會有幾乎相同的生命期,因此,這些生命期長的模態對於能量儲存上有著相同的貢獻,而且在能量儲存上比短生命期的共振腔有更好的效果,所以這些渾沌波幫助共振腔增加了儲存能量的能力。以有限差分時域分析法可以估計出運動場型共振腔相較於傳統共振腔有者將近兩倍的儲存能量的優點。
然而,這篇期刊介紹的應用層面不只在提高小型共振腔儲存能量的能力,就像前面提到的,運動場型共振腔對於量子球台系統是一個很有用的模型,適用古典波動的時間無關的亥姆霍兹方程式(Helmholtz equation) 與適用量子粒子的穩態薛丁格方程式(stationary Schrödinger equation) 具有相似處,可以幫助我們探討渾沌現象輔助下的量子效應,量子渾沌是一個有趣的研究領域,而且研究這些不同模態的生命期的收斂與它的量子對應將會是一個有趣的課題。
除了上述應用之外,此種渾沌共振腔也可以視為渾沌散射介質的一個例子,最近關於一任意排列金屬圓錐微波的渾沌散射的研究有幫助於瞭解類似海浪碎波的高振幅波,碎波在光學裡被報導起因於非線性效應中最近並且渾沌光學非線性共振腔建立關聯,無論由線性系統產生的光學碎波是否可以表現出波的渾沌現象(就好像前述中微波渾沌的散射實驗),都可以透過未來的渾沌共振實驗來進行研究。
|
資料來源: |
Marc Sciamanna, ”Optical resonators: Chaos aids energy storage,”
Nature Photonics 7, 430–431 (2013). doi:10.1038/nphoton.2013.135 Published online 30 May 2013
http://www.nature.com/nphoton/journal/v7/n6/full/nphoton.2013.135.html
|
|
|
|
|
|
註1:取自成大光電所”染料摻雜液晶注入毛細管產生雷射輸出之研究及應用”
http://ir.lib.ncku.edu.tw/handle/987654321/123331?locale=en-US
|
|
|
|
|
|
|