|
—
数据提供:影像显示科技知识平台 (DTKP, Display Technology
Knowledge Platform) —
—
整理:林晃岩教授、陈圣灏 —
浑沌帮助能量的储存
浑沌过程可以在动态系统中被观察到,它的结果会随着初始条件的不同而有很大的变化,1972年由Edward Lorenz 所提出「蝴蝶效应」的现象,之后陆续在各种书籍以及电影中流行起来。浑沌效应几乎在所有的科学领域中被提及;在光学领域中,例如当一道扰动的光经过一个充满非线性材料的共振腔,我们可以在此激光二极管的输出中观察到浑沌现象;还有,在高菲涅尔数(Fresnel numbers)的激光系统中,我们也可以在它的复杂时空型态(Complex spatiotemporal pattern)观察到浑沌现象。
一个具有浑沌现象的系统,它的结果是无法预测的,因此通常在系统中我们不希望有这种现象存在;然而,浑沌现象的一些特性对于改善光学系统的表现是有帮助的,例如:高维度光学浑沌中加入一个具有浑沌滤波性质的同步耦合振荡器,可以使得讯息以每秒Gb等级的速率在超过公里等级距离的光纤系统网络中作保密传输;除此之外,利用随机输出与应用适当的后制方法来操作激光,随机数产生的位元传输速率可以高于电子系统达到好几个数量级。最后,这种在非对称光学共振腔中的浑沌散射光之高乱度特性改善了微型共振腔激光的输出功率与光束的方向性。
现在,Liu等人在Nature Photonics中提出了光学浑沌的另一个好处
:它可以提高藉由宽带光源激发的共振腔能够储存的能量,这个好处在两个光学领域中引起了很大的兴趣,第一个是高质量因子(通常定义为共振腔储存的能量以及共振腔消耗的能量的比值)宽带光学共振腔的开发,体积小、质量因子高、自由频谱范围大的微型共振腔对于开发低阀值微型激光、极小滤波器和开关与腔内量子电动力学实验等是非常关键的;第二个则是让我们更了解浑沌共振腔—此共振腔的光学模态不受限于传统规律周期轨道的限制,例如圆形共振腔的回音廊模态(whispering gallery modes,注1),因此这种共振腔内的浑沌波有着非常多且复杂的光线轨迹,这种共振腔产生与动态台球的轨迹具有许多相似特性;也是一个探讨量子浑沌(例如浑沌穿隧)基本观念的极佳系统。
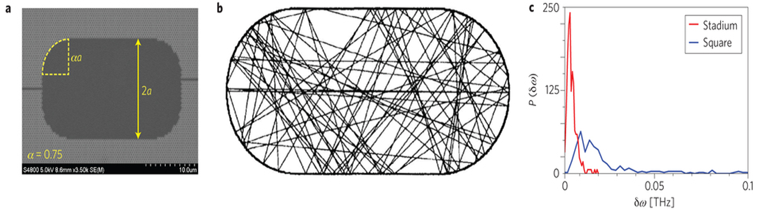
为了引进光学浑沌以及提高能量的储存,Liu 等人制作了许多变形的介电质光学共振腔,图1a为在一由在绝缘体上硅技术做成的平面光子晶体中的二维运动场型共振腔,研究学者设计此共振腔的几何形状和光子晶体的直径使它具有1500奈米的能隙同时还有大约400奈米的频宽,这种设计使得一个波长大约在1300到1700奈米的电磁波在此运动场型共振腔中不停地来回反射,后来Liu等人利用频谱分析的方法来量测输出中不同共振模态的谱线宽。
 |
|
图1、运动场型光学共振腔的浑沌模态 a. Liu等人利用扫描式电子显微镜扫描出的运动场型共振腔图像;b. 几何光学中运动场型共振腔之浑沌轨迹;c. 方形与球场型共振腔的腔场模态谱线宽的统计分布图。 |
|
|
|
图1b所展示的问题是由Bunimovich首先做数学研究,其中,一道光以任一角度进入运动场型系统后会在边界处经过许多次反射,此种光线具有复杂的浑沌轨迹;有两个具有质量的小球分别以两个稍微不同的起始位置进入球场型系统中,经由一段时间后,这两个小球的轨迹将会急遽的发散,而这种系统可以由正的黎阿普诺夫指数(positive Lyapunov exponent)来描述(此函数定义了相邻轨迹的发散程度),同样的,它也可以被描述为具有非零但有限的Kolmogorov–Sinai 乱度,考虑这种光学系统,它意味着运动场型共振腔相较于传统圆形或是长方形的共振腔可以有很大数量、生命期更长的光子共振模态,从耦合模态理论中我们可以发现共振腔中第i个模态的能量正比于光子的生命期如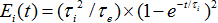 , ,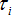 是第i个模态的生命期, 是第i个模态的生命期,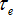 是此模态的逃脱速率,由于光子生命期与某一共振模态的谱线宽呈反比,谱线宽越窄的的模态场在运动场型共振腔中会比一般的方形共振腔的收集效果会更好。 是此模态的逃脱速率,由于光子生命期与某一共振模态的谱线宽呈反比,谱线宽越窄的的模态场在运动场型共振腔中会比一般的方形共振腔的收集效果会更好。
经过许多次量测不同形状、截面积为400到1200μm2之共振模态谱线宽后,Liu 等人在此一变形共振腔中确实观察到有更尖锐的峰值,此外,他们还发现所有模态的谱线宽几乎都会收敛至某一特定值,在图1c可以明显看出来,此图说明了球场型共振腔与方形共振腔某一谱线宽值与其机率的分布图,相较于方形共振腔,浑沌共振腔的谱线宽会往较小的值偏移,这不只说明了共振模态的光子生命期的增加同时也说明了所有模态最后都会有几乎相同的生命期,因此,这些生命期长的模态对于能量储存上有着相同的贡献,而且在能量储存上比短生命期的共振腔有更好的效果,所以这些浑沌波帮助共振腔增加了储存能量的能力。以有限差分时域分析法可以估计出运动场型共振腔相较于传统共振腔有者将近两倍的储存能量的优点。
然而,这篇期刊介绍的应用层面不只在提高小型共振腔储存能量的能力,就像前面提到的,运动场型共振腔对于量子球台系统是一个很有用的模型,适用古典波动的时间无关的亥姆霍兹方程式(Helmholtz equation) 与适用量子粒子的稳态薛丁格方程式(stationary Schrödinger equation) 具有相似处,可以帮助我们探讨浑沌现象辅助下的量子效应,量子浑沌是一个有趣的研究领域,而且研究这些不同模态的生命期的收敛与它的量子对应将会是一个有趣的课题。
除了上述应用之外,此种浑沌共振腔也可以视为浑沌散射介质的一个例子,最近关于一任意排列金属圆锥微波的浑沌散射的研究有帮助于了解类似海浪碎波的高振幅波,碎波在光学里被报导起因于非线性效应中最近并且浑沌光学非线性共振腔建立关联,无论由线性系统产生的光学碎波是否可以表现出波的浑沌现象(就好像前述中微波浑沌的散射实验),都可以透过未来的浑沌共振实验来进行研究。
|
资料来源: |
Marc Sciamanna, ”Optical resonators: Chaos aids energy storage,”
Nature Photonics 7, 430–431 (2013). doi:10.1038/nphoton.2013.135 Published online 30 May 2013
http://www.nature.com/nphoton/journal/v7/n6/full/nphoton.2013.135.html
|
|
|
|
|
|
注1:取自成大光电所”染料掺杂液晶注入毛细管产生激光输出之研究及应用”
http://ir.lib.ncku.edu.tw/handle/987654321/123331?locale=en-US
|
|
|
|
|
|
|