 |
Surface
Plasmons and Its Application in Plasmonic
Thermal Emitter (PTE) and Solar Cell
Professor
Si-Chen Lee
Graduate Institute of Photonics and
Optoelectronics, National Taiwan University
台湾大学光电所 李嗣涔教授
-
“Localized shape resonance on
silver film perforated by
H-shaped and more complex shaped
hole arrays”,
Hao-Fu Huang, Yu-Wei Jiang,
Hung-hsin Chen, Yi-Ting Wu, Yi-Tsung
Chang, Fang-Tzu Chuang, and
Si-Chen Lee,
Optics express, Vol. 19, Iss. 6,
pp. 5225–5231 (2011).
 |
 |
| (a) |
(b) |
|
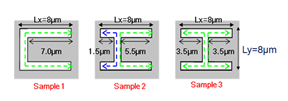
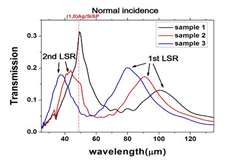
Fig. 1 (a) Top view and structure parameter of samples 1 to 3. (b) Zero-order transmission spectra at normal incidence of samples 1, 2, 3. The vertical red dash line represents the theoretical position of degenerated (1, 0) Ag/Si mode. |
-
“Wavelength Selective Plasmonic
Thermal Emitter by Polarization
Utilizing Fabry-Pèrot Type
Resonances”,
Pei-En Chang, Yu-Wei Jiang,
Hung-Hsin Chen, Yi-Tsung Chang,
Yi-Ting Wu, Lawrence Tzuang,
Yi-Han Ye and
Si-Chen Lee,
Appl. Phys. Lett., 98, 073111
(2011).
 |
 |
|
(a) |
(b) |
|
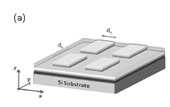
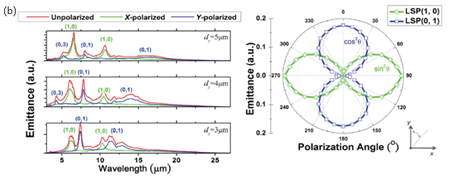
Fig. 2
The schematic view of
(a) a MIM PTE with
rectangular metallic
patch arrays as top
layer. (b) Emittance
spectra of three samples
with all
dx equal to 2
mm and
dy = 3, 4 and 5
mm, respectively.
The LSP (1, 0) and (0,
1) modes are at
wavelength of about 6
mm and 8
mm, respectively.
The green dotted curve
is a fit of LSP (0, 1)
to a
Sin2θ
dependence, while the
blue fit curve of LSP
(1, 0) to a
Cos2θ
dependence. |
-
“Hydrogenated Amorphous Silicon
Solar Cell on Glass Substrate
pattered by Hexagonal
Nano-Cylinder Array”,
Wei-Chen Tu, Yi-Tsung Chang,
Chieh-Hung Yang, Dan-Ju Yeh,
Chung-I Ho and
Si-Chen Lee,
Appl. Phys. Lett., 97, 193109
(2010).
Modal Characteristics of Antiresonant
Reflecting Pipe Waveguides for Terahertz
Waveguiding
Professor Hung-chun Chang
Graduate Institute of Photonics and
Optoelectronics, National Taiwan
University
台湾大学光电所 张宏钧教授
The pipe waveguide is promising for
terahertz (THz) waveguiding owing to its
low-loss feature and simple structure. In
this work, modal characteristics of the
leaky core modes of the pipe waveguide are
investigated in the THz range. Utilizing the
finite-difference frequency-domain (FDFD)
mode solver, modal indices and attenuation
constants of the core modes which are
frequency dependent are calculated for
different core diameters, cladding
thicknesses, and cladding refractive
indices. It is found that at certain
frequencies no core modes can exist.
Comparing these frequencies with the
resonant frequencies of the cladding reveals
that the guiding mechanism of the core modes
is that of the antiresonant reflecting
guiding. Calculated results also suggest
that, to have a low-loss and high-bandwidth
pipe waveguide, large core diameter, thin
cladding thickness, and low refractive index
are desired. The effect of material
absorption is also examined, which shows
that the attenuation constant magnitude will
be increased and the increment is more
significant at higher frequencies. Moreover,
modal patterns are shown for the fundamental
mode and the higher order modes, including
modal intensity distributions and electric
field vector distributions. It is observed
that modal patterns of the core modes of the
pipe waveguide resemble those of the guided
modes of the step-index fiber. From the
spectrum of the attenuation constant, it
shows that the fundamental mode (HE11-like)
has the smallest attenuation constant and is
the dominant mode for the pipe waveguide
investigated. Using time-domain spectroscopy
to measure the transmission spectra of PMMA
pipes in collaboration with Prof. Chi-Kuang
Sun, guiding mechanism of the pipe
waveguides was experimentally confirmed to
be that of antiresonant reflecting guiding.
(Optics Express, vol. 18, no. 1,
pp. 309–322, 22 January 2010.)
|
 |
|
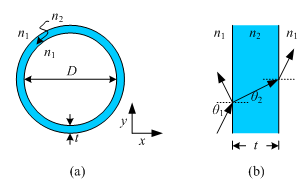
Fig. 1. (a) Cross-section of the
pipe waveguide, where
n1 = 1
(air). (b) The cladding can be
viewed as a Fabry-Perot etalon. |
|
|
 |
|
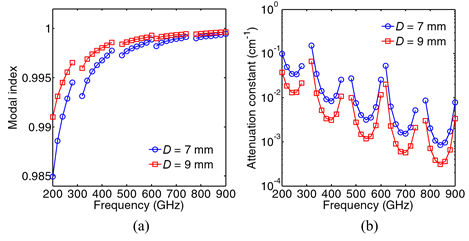
Fig. 2. (a) Modal indices and
(b) attenuation constants of the
fundamental core mode of the
pipe waveguide for D =
7 mm and 9 mm. |
|
|
 |
|
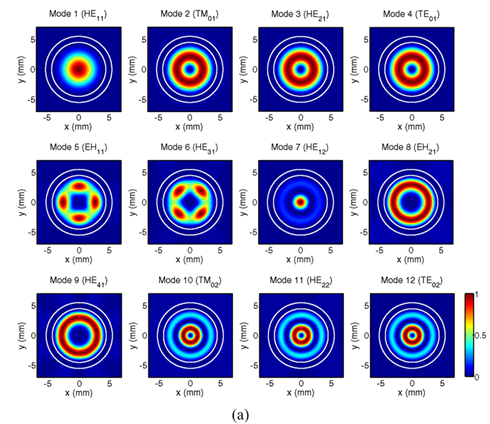
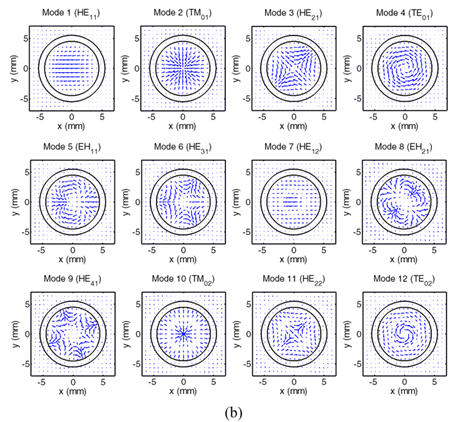
Fig. 3. (a) Modal intensity
distributions and (b) electric
field vector distributions of
the first twelve lowest modes of
the pipe waveguide at 380GHz. |
|
|
 |